医師国家試験・内科専門医・総合内科専門医によく出る統計の計算
試験に出てくる統計の問題は、実臨床の時に感度や特異度以外はあまり使わない知識なので、毎回確認する必要がありますよね。
今回は試験に出てくる部分についてだけ、端的にまとめていますのでぜひ参考にしてみて下さい。
有病率・感度・特異度・有病率・オッズ・陽性尤度比(ゆうどひ)・検査後確率など
統計の問題でよく出る用語に有病率・感度・特異度・有病率・オッズ・陽性尤度比(ゆうどひ)・検査後確率などがあります。
聞いたことはあっても、どうやって計算するのかは試験のたびに覚えなおさなければいけません。
特に、尤度比(ゆうどひ)の計算は覚えていないと、自分ではなかなか計算できません。
以下に、代表的なものの計算方法や、言葉の意味について解説した表を掲示します。
試験前に確認するようにしましょう!

| 有病率 | (A+C) / (A+B+C+D) | 対象全体のうち疾患のある人の割合 |
| 感度 | A / (A+C) | 疾患のある人が検査で陽性になる確率。 感度が高いと見逃しにくくスクリーニングによい。 |
| 特異度 | D / (B+D) | 疾患のない人が検査で陰性になる確率。 特異度が高いと偽陽性が少なく、確定診断によい。 |
| 陽性的中率 | A / (A+B) | 検査が陽性の時に疾患がある確率。 |
| 陰性的中率 | D / (C+D) | 検査が陰性の時に疾患がない確率。 |
| 陽性尤度比 | 感度 / (1-特異度) | positive likelihood ratio= +LR 疾患のある人がない人に比べて何倍検査で陽性になりやすいか |
| 陰性尤度比 | (1-感度) / 特異度 | negative likelihood ratio = -LR 疾患のある人がない人に比べて何倍検査で陰性になりやすいか |
| 検査前オッズ | 有病率 / (1-有病率) または (a+c) / (b+d) | 疾患がない人に比べて、疾患がある人が何倍いるか |
| 検査後オッズ(検査陽性の時) | 検査前オッズ × 陽性尤度比 | 検査で陽性の場合、疾患がない人に比べて、疾患がある人が何倍いるか |
| 検査後確率 | 検査後オッズ / (1+検査後確率) | 検査で陽性の場合の、その疾患がある確率 |
実際に計算してみよう!
たとえば、以下のようなデータの場合のそれぞれの計算方法、価を掲示します。
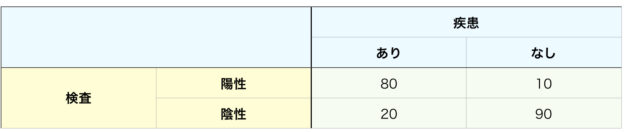
有病率=(80+20)/(80+20+10+90)=100/200=0.5
感度=80/(80+20)=0.8
特異度=90/(10+90)=0.9
陽性的中率=80/(80+10)=0.889
陰性的中率=90/(20+90)=0.81
陽性尤度比=0.8/(1-0.9)=0.8/0.1=8
陰性尤度比=(1-0.8)/0.9=0.222
検査前オッズ=0.5/(1-0.5)=0.5/0.5=1
検査後オッズ=1×8=8
検査後確立=8/(8+1)=0.889
例題を解いてみましょう
例題)(表の数字は適当です)
入院中の患者が発熱して尿路感染症を疑っている。
この状態で検査したの各割合は以下の表のとおりです。
この患者が検査で陽性だった場合、尿路感染症である可能性は何%でしょうか?

解説)
有病率=(80+20)/(80+20+10+90)=100/200=0.5
感度=80/(80+20)=0.8
特異度=90/(10+90)=0.9
陽性尤度比=0.8/(1-0.9)=0.8/0.1=8
検査前オッズ=有病率/(1-有病率)=0.5/(1-0.5)=0.5/0.5=1
検査後オッズ=検査前オッズ×陽性尤度比=1×8=8
検査後確立=8/(8+1)=0.889
答え)約89%
医療系の統計問題まとめ
上の例題がスラスラ解けるようになれば、医師国家試験や内科専門医・総合内科専門医の一般的な統計問題は解けるようになるでしょう。
ほかにも統計の問題はNNT(number needed treet)なども出るので、そちらもいつか記事にしますね。
みなさんの試験勉強の一助になれれば幸いです。
よければtwitterもしているのでフォローお願いします!


